«Can I know a cycle, / according to nature round, / and never complete?»

«Posso conoscere un cerchio, / per natura rotondo, / e mai completo?»

Haiku in lingua inglese

Una sola lettera dell’alfabeto greco per così tante cifre. Quante, per l’esattezza? Per rendere l’idea, provo a contare quante pagine è lunga l’appendice di una monografia: per elencare appena diecimila cifre impiega ben sette pagine. Forse a questo punto vi starete chiedendo: c’è allora un limite alla conoscenza di tutti i decimali di π?

Il Pi greco affascina da secoli i matematici, e non solo. Molti hanno tentato di strappargli quanti più decimali, nella speranza di riuscire a disvelarne l’intera spirale anche grazie al proprio contributo. In effetti, anche se addentrarsi nei meandri di un numero così labirintico può apparire un’occupazione riservata a specialisti e appassionati, scopriremo che la sua presenza nelle nostre vite è più significativa di quanto non crederemmo, e vedremo come tutto questo si lega all’infinito. Innanzitutto, però, delineiamo un profilo di π.

GENERALITà DI π

Per quanto a noi possa sembrare scontata l’associazione del nostro numero alla lettera greca π, non fu sempre così. Alle varie oscillazioni relative alla denominazione pose fine nel 1706 l’opera Synopsis Palmarium Matheseos, di William Jones, e l’autorevolezza di Euler (che pure aveva avuto delle esitazioni) consacrò definitivamente il simbolo di π. Perché proprio questa lettera? In quanto prima lettera del vocabolo greco “periféreia”, che significa “circonferenza”. Secondo altri, invece, un omaggio a Pitagora. D’altro canto, non dobbiamo immaginare π come univocamente vincolato a questo uso, in matematica: ad esempio, è presente nella funzione π(x).

Da un punto di vista strettamente matematico, è bene tenere presente che:

• π è classificabile come numero irrazionale (ovvero un numero decimale illimitato non periodico);

• π è inoltre un numero trascendente (ossia non è soluzione di nessuna equazione di tipo polinomiale con coefficenti razionali);

• a titolo di curiosità, si ipotizza che π possa appartenere anche al gruppo dei numeri normali, oltre che ad altri ancora!

• è possibile considerare π come una costante matematica, che si esprime come doppio della relazione fra l’area di un cerchio (πr²) e l’area del quadrato in esso inscritto (2r²):

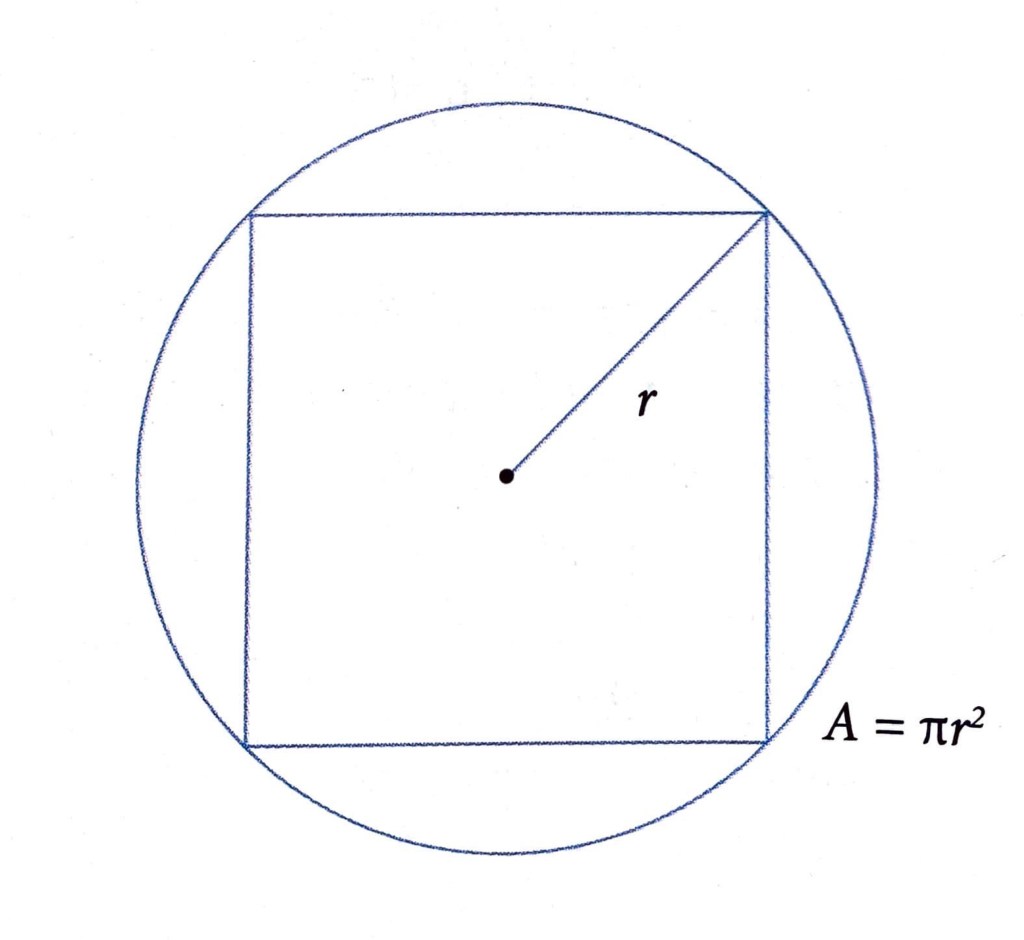
Non solo: la costante si esprime anche come rapporto costante tra lunghezza della una circonferenza (p) e il suo diametro (d): p/d= π

La quadratura del cerchio

Ciò che interessava maggiormente i matematici antichi era costruire una superficie quadrata che fosse equivalente a una circolare. Questo avrebbe consentito di effettuare misurazioni in modo molto più pratico – misurare un’area quadrata è molto più immediato che misurarne una circolare. La quadratura del cerchio corrisponde precisamente a questo: ottenere graficamente l’equivalente quadrato di una circonferenza, adoperando solo riga e compasso. In termini matematici si può tradurre nel seguente modo:

πr²=l²

Dunque π diveniva cruciale nella questione: riuscire a calcolare il suo valore era necessario per risolvere il problema. Infatti, era in primis questo l’obiettivo che si prefiggevano molti di quanti ricercarono infaticabilmente decimali di π nel corso della storia.

Fu questa, insomma, una sorta di quête secolare. Ripercorriamo insieme le sue tappe, e scopriamo l’eventuale risoluzione del problema, sempre che ce ne sia una.

π, la costante di Archimede

Archimede raggiunse risultati notevoli, avvalendosi del metodo di esaustione, senza conoscere gli odierni strumenti di limite e integrale.

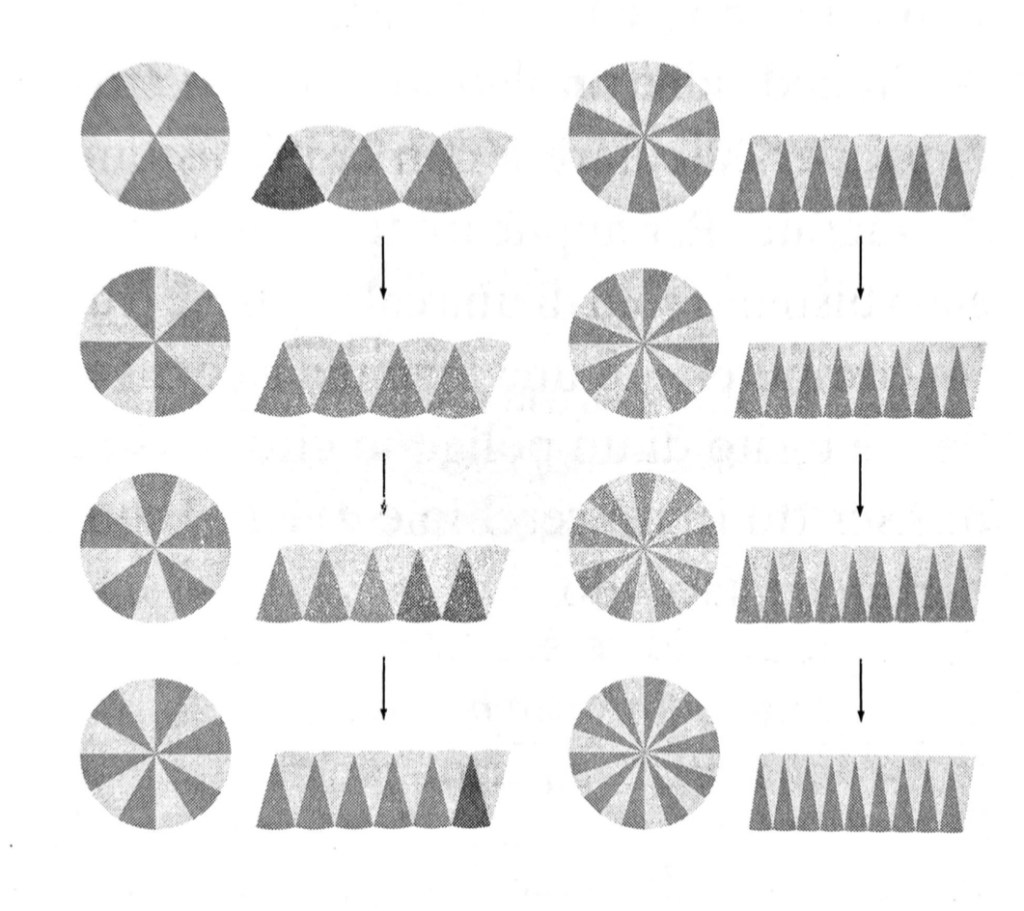
In questo articolo potrete trovare illustrato questo semplice ma ingegnoso metodo. Qui di seguito, invece, percorreremo un sentiero più moderno, molto affascinante, e appena un po’ impervio (non temete, nulla di cui non si possa venire a capo con un po’ di concentrazione).

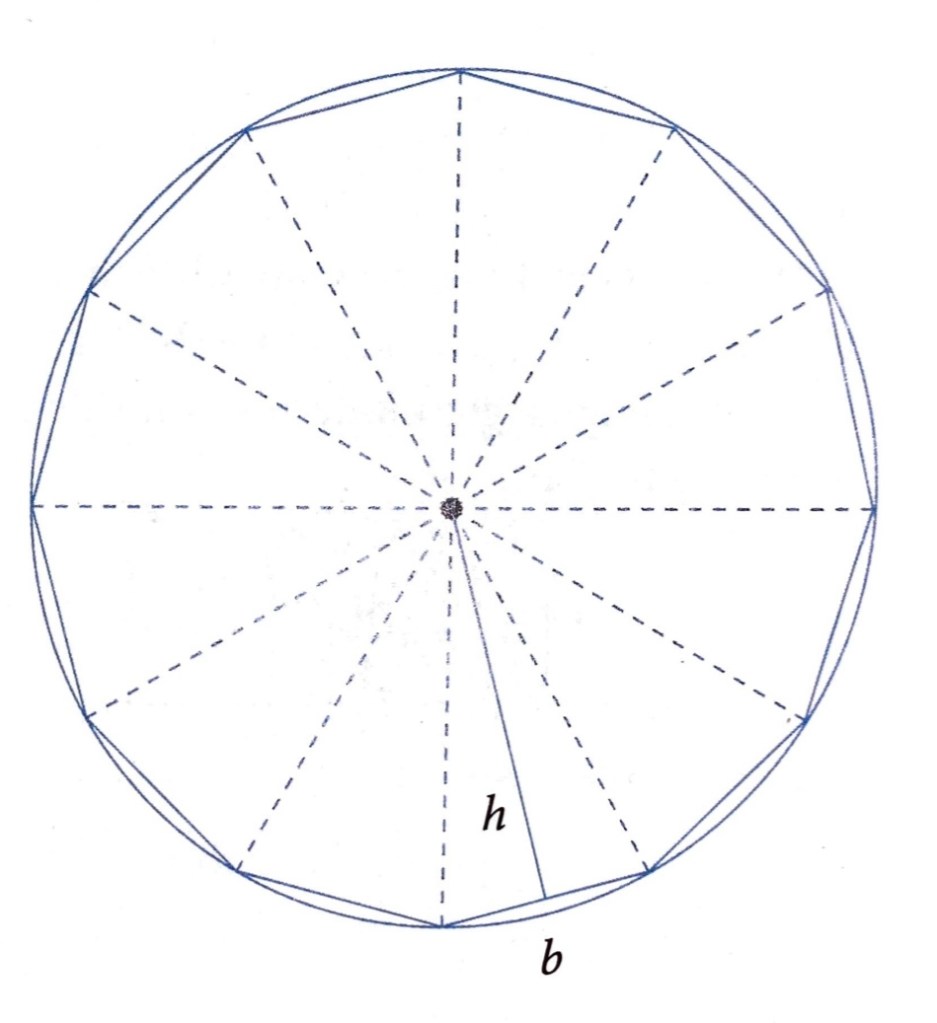
Abbiamo qui vari triangoli – vari “spicchi” –, di base b e altezza h. L’area totale degli n (con cui indichiamo un numero generico) triangoli è molto vicina a quella del cerchio, lo si può vedere dal disegno. Sarà pari a:

A_n= n(area triangolo), ovvero

Ora portiamo l’uguaglianza al limite:

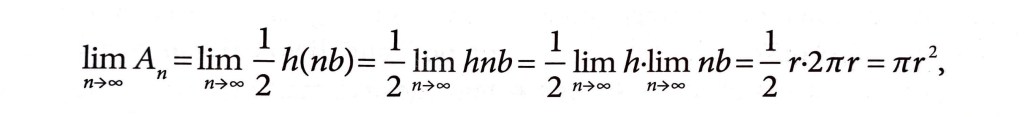
Infatti, e di questo possiamo avere una conferma visiva, l’altezza del triangolo (h) si avvicina molto a quella del raggio della circonferenza, come la somma di tutte le basi (b) si avvicina molto al perimetro della circonferenza; quanti più triangoli si hanno (aumenta n), tanto più quest’impressione si acuisce. A maggior ragione se n tende ad infinito.

Perciò, giungiamo alla conclusione che:

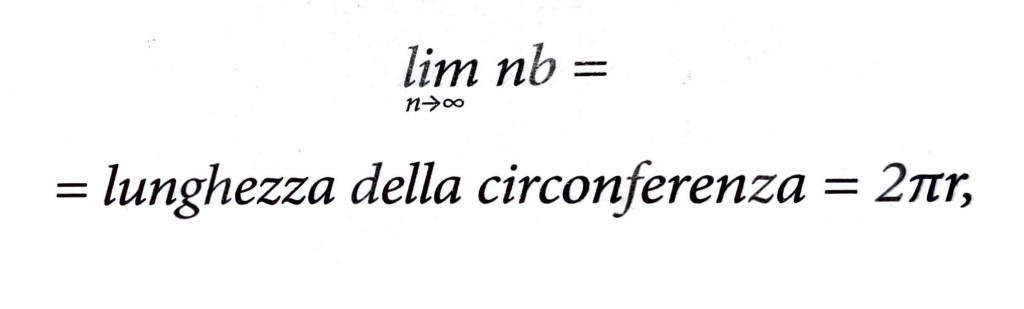
In questo modo, siamo in grado di ottenere un’approssimazione della lunghezza della circonferenza, e dunque di π stesso.

Tornando ad Archimede, a lui dobbiamo la seguente approssimazione del valore di π:

3,140845… < π < 3,142857…

Si tratta di un risultato estremamente soddisfacente, per i tempi. Consideriamo per un momento che il matematico siracusano non conosceva il moderno calcolo integrale. Non solo, per effettuare i suoi calcoli (adottò una formula ricorsiva, nota come algoritmo di Archimede) non disponeva certamente di una calcolatrice. Ciononostante giunse a calcolare fino al perimetro di un poligono di novantasei lati.

Dopo Archimede

Vitruvio, Tolomeo, il Fibonacci, e molti altri matematici, anche orientali, si accostarono al calcolo di π. Degno di nota è il risultato ottenuto nel 1424 da Jamshīd al-Kashī. Per la prima volta, per calcolare π, si servì di una serie, uno strumento sommatorio di lunghezza infinita: un calcolo numerico puro, dunque. La formula dovette tuttavia passare alla storia come “formula di Leibniz“. Con essa, riuscì a calcolare π con un’approssimazione corretta di 16 cifre.

Approdiamo ora agli inizi del Settecento, con un balzo temporale piuttosto ampio. Ai nomi di Leibniz e di Newton si lega inscindibilmente l’introduzione dell’analisi infinitesimale. Entrambi, menti straordinariamente eclettiche, si diedero una strenua quanto ostinata contesa in merito alla paternità di una tale innovazione, davvero di portata rivoluzionaria. Ne sorse una vera e propria querelle (sui cui dettagli potete informarvi qui, e qui), di fatto irrisolta.

Nel frattempo, non era ancora sopito il desiderio di dimostrare la praticabilità della quadratura del cerchio. Il filosofo inglese Hobbes dichiarò nel De corpore (1655) di essere riuscito nell’impresa, ma fu prontamente smentito da John Wallis (proprio lui, l’inventore del simbolo dell’infinito). Anche in questo caso, sorse un’aspra controversia. Nel 1667, invece, James Gregory tentò di dimostrare l’impossibilità della quadratura, ma fallì. Dei suoi pur considerevoli risultati si avvalse però Abraham Sharp, per giungere a calcolare 71 decimali corretti di π, nel 1699.

È importante sottolineare che non erano solo matematici di professione, accademici, a interessarsi di simili questioni. William Shanks, matematico dilettante, offrì nel 1873 un contributo straordinario al calcolo di π, computando ben 707 cifre, pur essendo in parte errate, tanto da esserne omaggiato in un fregio del Palais de la Découverte di Parigi.

A distanza di poco più di un secolo, nel 2002 il calcolo è arrivato a 1 241 100 000 000 cifre, grazie a Yasumasa Kanada, che si è servito di un supercomputer Hitachi. Un progresso certamente impensabile senza l’ausilio di strumenti informatici sempre più efficienti.

L’utilità di π

Il Pi greco, generalmente, entra a far parte della nostra quotidianità molto presto: le formule che impieghiamo per calcolare l’area e il perimetro del cerchio ci vengono insegnate sin da bambini. Sono davvero molte le formule in cui compare e, nel caso delle formule seguenti, si può riscontrare, oltre che una bellezza intrinseca, anche un certo fascino esteriore, in grado di colpire l’occhio con immediatezza:

• Il “prodotto infinito” di John Wallis:

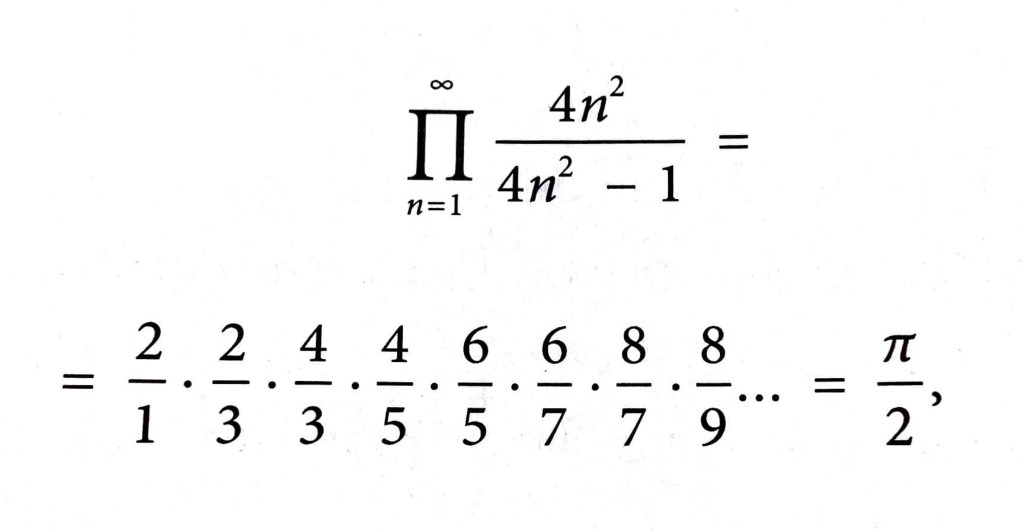
• Il “prodotto infinito” di Viète, rielaborato matematicamente da J. Munkhammar:

• Le frazioni continue, come quella di Lambert:

• e, per concludere, quella che fu considerata la formula più bella da R. Feynmann, in quanto riassume in sé le cinque costanti più notevoli della matematica:

e^iπ + 1 = 0

Sapevate che i lettori della rivista The Mathematical Intelligencer la votarono come la formula più bella della matematica? (Qui potete rileggere l’articolo in cui veniva proposto il sondaggio, qui i risultati).

Ma naturalmente π si rivela essere prezioso in molti altri ambiti. Nella probabilità e la statistica, che hanno ripercussioni sugli aspetti più pratici della nostra vita, π ha un’incidenza decisiva. Distribuzione della statura, coefficiente intellettivo, errori strumentali dei telescopi, etc. etc.: in tutto questo π gioca un ruolo considerevole.

A suggello di questa breve rassegna, ricordiamo che, secondo Einstein , π è un numero fondamentale nella descrizione dell’universo, interessando fenomeni naturali descritti da leggi che riguardano tutto ciò che abbia a che fare con la forma circolare.

UNA quête FALLIMENTARE…

A dimostrare la trascendenza di π fu Lindemann, nel 1882: il numero veniva così escluso dall’ambito geometrico. Da questo conseguì la consapevolezza che la quadratura del cerchio era una mera utopia.

Questo non impedì a molti aspiranti “quadratori” di desistere, neppure dinanzi all’evidenza. Il caso più eclatante, forse, fu quello di una proposta di legge redatta nel 1897 dal matematico dilettante J. Goodwin, il quale sosteneva senz’altro di aver risolto il problema della quadratura, e proponeva l’introduzione a titolo gratuito del suo nuovo metodo nelle scuole dell’Indiana. L’iter parlamentare che avrebbe portato alla sua approvazione fu interrotto soltanto dal fortuito intervento di un accademico.

Tuttavia, non bisogna dimenticare che è sempre possibile cercare delle approssimazioni, proprio come fece il visionario matematico Ramanujan, con sorprendente esattezza. Un gesto estremamente umano, quello di tentare di approssimarsi all’inarrivabile quanto più possibile, nella piena coscienza dei propri limiti.

Più di un numero

Come abbiamo visto, questa è anche una storia di aspre contese tra studiosi, riforme legislative, fanatismo dilettantesco, eterea bellezza.

La realtà è che si tratta di qualcosa di più di un numero, per ciò che cela dietro un simbolo, per la sua attitudine unica a catalizzare l’interesse di menti di ogni epoca, e per le implicazioni filosofiche e anche pratiche che possono scaturire dall’approfondimento dei suoi illimitati decimali.

Insomma, π è in qualche modo assunto come emblema della ricerca per la ricerca. Di qui l’istituzione del Pi-day, sapevate della sua esistenza? La data non poteva che essere il tre marzo, dal momento che ripropone le prime tre cifre di π (03/14). Anche un’azienda come Google giunse a emettere la stessa cifra di azioni dei primi otto decimali di questo numero (ovvero 14.159.265).

Ma forse la curiosità più sorprendente è che esiste un cercatore computerizzato di cifre di π (The π searcher) per rintracciare nella sua espressione decimale una sequenza desiderata. Perciò, oltre all’ameno passatempo di rintracciarvi la propria data di nascita, questi strumenti consentono di dedicarsi a interessanti ricerche: la labirintica spirale di decimali di π cela al suo interno delle affascinanti iterazioni. Un esempio: le cifre “40” compaiono nella posizione “70”, che a sua volta compare nella posizione “96”, e così via fino a ritornare, ciclicamente, alle cifre “40”.

Ma questa è anche una storia di arte e poesia. A π, numero incredibilmente affascinante si sono ispirate alcune opere d’arte contemporanea, come quelle che proponiamo:

Ingegni più inclini all’arte della parola hanno invece composto versi che consentano di tenere a mente quante più cifre più cifre possibili di π. È proprio il caso della nostra citazione di apertura, un haiku in cui il numero di lettere di ogni parola corrisponde a una cifra di π…verificare per credere!

Alcuni versi, puramente tesi a fini mnemonici, sfociano nel non-sense. Altri sono estremamente significativi, come Il gran numero del premio Nobel Wisława Szymborska (1966):

Il serpente più lungo della terra dopo vari

metri si interrompe.

Lo stesso, anche se un po’ dopo, fanno

i serpenti delle fiabe.

Il corteo di cifre che compongono

il Pi greco

non si ferma sul bordo della pagina,

È capace di srotolarsi sul tavolo, nell’aria,

attraverso il muro, la foglia, il nido,

le nuvole, diritto fino al cielo,

per quanto è gonfio e senza fondo il cielo.

Follow Ápeiron on Instagram:

• Instagram