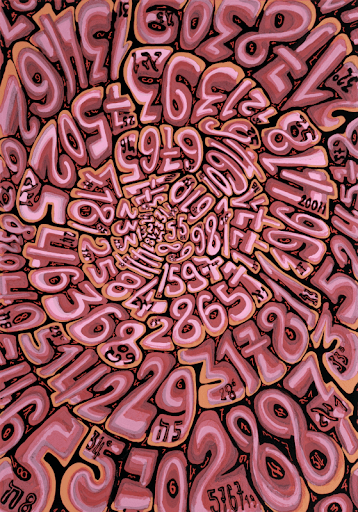E adesso l’essenza del Linguaggio del Mondo era lì, davanti ai suoi occhi: non aveva dovuto interpretare frasi astruse o disegni costellati di spiegazioni, perché l’Universo non aveva alcun bisogno di spiegazioni per proseguire il proprio cammino nell’infinito.

Paulo Coelho

Nonostante il costante e sempre più preponderante richiamo costituito dalle coeve istanze materialistiche, l’arte del Novecento non poté a lungo fare a meno di confrontarsi con l’infinito, essendo un concetto rispondente ad un anelito di libertà connaturato nell’uomo, e unico mezzo tramite cui prendere le distanze dalle brutture della quotidianità: insomma un concetto insostituibile e impossibile da ignorare.

Sala XI: Gli squarci di libertà di lucio fontana

La rappresentazione dell’infinito continua a costituire un’attrattiva per gli artisti che operano nel secondo dopoguerra nell’ambito dell’Arte informale. In questo contesto l’evento artistico viene ricondotto all’atto creativo stesso, esplicitato dalla materia e dal gesto. Su quest’ultimo artisti come Fontana pongono l’accento in modo particolare: l’arte non si identifica propriamente e tradizionalmente nel prodotto artistico, bensì nella sua esecuzione. Inoltre, nel caso di Lucio Fontana, lo spazio della tela, ora rientrante, ora sporgente, è posto in rapporto diretto con lo spazio e la luce reali: dunque il gesto caratteristico, che consiste nello squarciare o forare la tela per mezzo di lame di rasoio, si fa rappresentazione e ricerca, al contempo, di un’apertura verso uno spazio infinito.

Sala XII: Le visioni paradossali di Maurits Escher

«L’uomo è incapace di immaginare che in qualche punto al di là delle stelle più lontane nel cielo notturno lo spazio possa avere fine, un limite oltre il quale non c’è che il “nulla”. Il concetto di “vuoto” ha per noi un certo significato, perché possiamo almeno visualizzare uno spazio vuoto, ma il “nulla” nel senso di “senza spazio” è al di là delle nostre capacità d’immaginazione. È per questo che da quando l’uomo è venuto a giacere, sedere, stare in piedi, a strisciare e camminare sulla terra, a navigare, cavalcare e volare sopra di essa (e lontano da essa), ci siamo aggrappati a illusioni, a un al di là, a un purgatorio, un cielo e un inferno, a una rinascita o a un nirvana, che esistono tutti eternamente nel tempo e interminabilmente nello spazio».

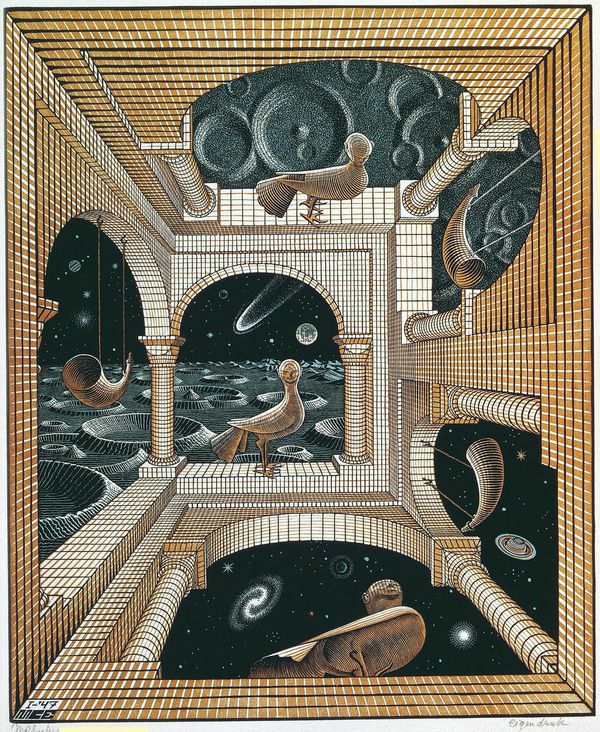
Queste le parole che Maurits Cornelis Escher espresse sul concetto di infinito nel 1959. Fu così che il maestro delle forme impossibili e di un approccio del tutto paradossale al concetto di spazio si avventurò nelle profondità dell’infinito. Non soltanto attraverso la tecnica della tassellatura, di cui risente ad esempio “Two birds” (figura n.6), ma anche attraverso forme geometriche spiralizzate (figura n.2 e 3). Ancora, l’incisore olandese concepisce costruzioni in cui v’è la presenza di un motivo sottoposto ad una progressiva riduzione radiale, convergendo verso il centro e sconfinando nell’infinitamente piccolo, come si verifica nella figura n. 7 e, in modo particolare, in “Limite del quadrato” (figura n.11), realizzato secondo la tecnica della “riduzione dall’interno all’esterno”. A questo proposito, scrisse:

«Dopo questa relativa soddisfazione del mio impaziente desiderio di una composizione che divenisse il simbolo dell’infinito (realizzata nella forma migliore in Limite del cerchio III), cercai di sostituire un quadrato al posto del cerchio – poiché le pareti rettilinee dei nostri spazi la richiamavano». 

Non solo. Escher interpreta il concetto di infinito anche attraverso cerchi concentrici, in cui la distanza dell’uno rispetto all’altro diminuisce progressivamente all’avvicinarsi al centro. Si tratta, in matematica, della spirale logaritmica (la stessa che Bernoulli definì “meravigliosa”, per la sua prerogativa “prodigiosa” di non avere né inizio né fine). Il medesimo principio, invertito, è presente in “Vortici“ (figura n.12), dove alcuni pesci sembrano essere risucchiati da un gorgo che descrive il grafico di un’omografia lossodromica (ovvero la curva inversa alla spirale logaritmica). Per quanto quasi involontariamente, appare evidente che la matematica costituisca l’ossatura delle opere di Escher, il quale giunse ad affermare: “Mi sento spesso più vicino ai matematici che ai miei colleghi artisti”.

Delle figure spiralizzate di Escher è stato detto che sembrano realizzare visivamente il concetto di “Strano Anello” (secondo una denominazione di Douglas Hofstadter), presente nei canoni bachiani, per esempio, e che si esplica quando, salendo o scendendo lungo i gradini di un sistema che sia gerarchico, ossia ordinato secondo un qualche criterio (come nel caso di una scala musicale, con i suoi gradi, o delle scale rappresentate dall’incisore olandese), ci si ritrovi paradossalmente al punto di partenza.

Opere come la celeberrima”Relatività” (figura n.1), e molte altre (figure n.4, 5, 8, 9, 10) riflettono l’influenza pervasiva delle scoperte rivoluzionarie compiute da Albert Einstein, in virtù delle quali, essenzialmente, lo spazio-tempo è condizionato dal sistema di riferimento.

Escher, in ultima analisi, riesce a trasmettere il carattere più sconvolgente dell’infinito, concetto che trasmette un senso di vertigine, un brivido intellettuale, nel momento in cui ci si trova dinnanzi ad una costruzione paradossale, ossia, nel senso etimologico del termine, “che va contro l’opinione” che ci siamo formati del mondo circostante, e che sconfessa la familiarità che abbiamo con il mondo.

Sala XIII: “Rooms by the sea” di Edward Hopper

Meriggiare pallido e assorto
presso un rovente muro d’orto,
ascoltare tra i pruni e gli sterpi
schiocchi di merli, frusci di serpi.

[…]

E andando nel sole che abbaglia
sentire con triste meraviglia
com’è tutta la vita e il suo travaglio
in questo seguitare una muraglia
che ha in cima cocci aguzzi di bottiglia.

Eugenio Montale, Merigiare pallido e assorto, da Ossi di seppia

Come è ricorrente nelle opere di Hopper, questo quadro, realizzato nel 1951, presenta un’opposizione tra interno ed esterno, e una porta aperta direttamente sul mare. Non a caso, questo è forse il dipinto di Hopper dalle tinte più surreali, visto lo straniamento prodotto da una soglia che non è barriera invalicabile, ma che, per essere oltrepassata, implica effettivamente il rischio di un salto, dell’annientamento nell’interminabile e profondo mare. Al contrario, la luce può introdursi nella stanza altrimenti completamente desolata – come viene sinistramente evidenziato dalle zone in ombra.

Non tutti i critici concordano nel ridurre l’opera hopperiana a mera rappresentazione di incomunicabilità, alienazione dell’uomo nella società contemporanea (in quel momento stretta nella morsa del bipolarismo della Guerra fredda, e dalla incessante minaccia di una guerra atomica), quasi si trattasse di una muraglia, di un limite invalicabile. Senz’altro è presente un ostacolo tanto paradossale – quale è una porta spalancata – da impedire una congiunzione con l’infinito. Tuttavia l’artista pone davanti all’osservatore l’attesa stessa di una rivelazione, di un messaggio salvifico (tematiche molto vicine al Montale di Meriggiare pallido e assorto e de I limoni; potremmo arrischiarci a dire che anche in quest’ultimo componimento è il giallo dei limoni, come nel caso della luce qui dipinta, ad incarnare l’epifania). La luce, la cui sorgente non viene mostrata, e la luce sola, è in grado di valicare il confine che separa lo spazio interno da quello esterno. Spadaro avrebbe detto che si tratta dell’ “ingresso in scena, sorprendente e imprevedibile, di una qualche forma di «salvezza».”

Sala XIV: Arte frattale

I frattali sono oggetti geometrici rinvenibili in natura di straordinario fascino. Essendo riconducibili a funzioni matematiche, è possibile, con l’ausilio di specifici software, dare luogo a spettacolari creazioni artistiche. Ne abbiamo proposto alcuni tra i più bei esempi.

Più dettagliatamente, i frattali impiegati a fini artistici possono essere suddivisi in macro-categorie:

1. quelli per cui esiste una regola di sostituzione geometrica (ad esempio la polvere di Cantor e la curva di Koch);
2. quelli generati da processi stocastici e non deterministici (come i paesaggi frattali);
3. quelli per cui può essere determinata l’appartenenza di un punto ad un insieme frattale tramite l’applicazione iterativa di una semplice funzione (ad esempio l’insieme di Mandelbrot e il frattale di Lyapunov);
4. quelli creati con sistemi di funzioni iterate (su tutti, le fiamme frattali).

Essi sono impiegati perfino per le animazioni digitali (un esempio? Nel noto cartone animato Frozen!) 

Sala XV: Tobia Ravà, dove l’arte incontra la matematica

“Tutto è numero”

Pitagora

Tobia Ravà, artista padovano, è da sempre sensibile all’intima connessione che può instaurarsi tra arte ed epistemiologia, e dunque tra ciò che appare – la raffigurazione – e il suo significato intimo ed ultimo.

Da tali premesse si origina uno stile del tutto originale, la cui cifra sono le cosiddette “texture alfa-numeriche” di cui si sostanziano arbusti, monumenti, boschetti , farfalle e perfino i canali veneziani, tavolta affini a disegni di tipo frattale. Pervasiva è la presenza della cultura ebraica, attraverso la presenza del suo alfabeto (inevitabile pensare all’Aleph di Borges…),coniugata con quella tipicamente veneta e, in ultimo, mitteleuropea, a restituire un’atmosfera unica ed inconfondibile. L’osservatore si trova perciò ogni volta al cospetto di un’opera dalla duplice lettura: da un lato la ghematrià, dall’altro la kabbalah, la “ricezione” di quello che è un sentiero spirituale, uno spunto di riflessione etico-filosofica.

Sembra dunque tradotto su tela il motto pitagorico per cui il numero è il principio concreto, l’unità di misura che accomuna tutte le cose (potete approfondire questi aspetti qui), ricreando così un’armonia cosmica, tra uomo e natura.

Tobia Ravà espone le proprie opere una serie di mostre dall’emblematico titolo “Memorie di infinito”. È possibile avere maggiori informazioni consultando il suo sito personale.

Sala XVI: “Descension” di Anish Kapoor

Concludiamo la nostra visita alla “Galleria dell’infinito” con un’ardita installazione di Anish Kapoor, realizzata nel Brooklyn Bridge Park.

I flutti neri che turbinano in modo vorticoso sono certamente molto allusivi. Da un lato il richiamarsi alla vite perpetua di Archimede, e dunque ad un principio di infinito di natura strettamente fisico-meccanica, dall’altro l’idea per cui l’osservatore si senta quasi risucchiare in quel vortice, perdendosi nel vuoto oscuro dell’infinitezza spaziale, originato proprio da un ciclico movimento della massa d’acqua, come se si trattasse di un “naufragar” non più “dolce”, ma assai sinistro, in un buco nero.

Una curiosità: anche in Italia Kapoor ha riproposto questa installazione, presso la Galleria Continua di San Gimignano.

Follow Ápeiron on Instagram:

• Instagram