Vari sono i simboli nei quali è racchiuso il concetto d’infinito, che tende a sfuggire alla nostra comprensione. La forma di “otto sdraiato”, così come la conosciamo, e adoperata nel mondo matematico, fu ideata da John Wallis, ma già in precedenza esistevano simboli molto simili a quello noto a tutti, ossia “∞”.Vediamo di ripercorrere in rassegna la “storia della notazione” di tale concetto.

UROBÓROS (1600 a.C.): Una prima rappresentazione del concetto di infinito si può trovare nel cosiddetto “Urobóros”, simbolo antichissimo, diffusosi in diverse culture,

dalla storia molto interessante. Il termine è di derivazione greca, e significa “serpente che si morde la coda”. Dunque, per quanto riguarda la rappresentazione, esso raffigura un drago, o un serpente, che, nel mordersi la coda, forma un circolo, che non ha né inizio né fine. In effetti, il simbolo si rivela particolarmente efficace: esso rappresenterebbe l’infinito come il ripetersi incessante di tutte le cose. Il serpente che si divora infatti indica la disgregazione e al contempo la rinascita (lo stesso avveniva, secondo la leggenda, alla Fenice, che rinascerebbe dalle sue stesse ceneri). La natura ciclica delle cose era particolarmente cara ai popoli precristiani, in particolare a quelli orientali. Basti pensare alla teoria del divenire del filosofo Eraclito (del pánta rheî), o quella di Anassimandro. Per questo motivo, il simbolo rappresenta l’unità primigenia, la totalità del tutto, e dunque anche l’infinito. Tale simbolo potrebbe ben rappresentare anche la teoria dell’ “eterno ritorno” del filosofo Nietzsche. La più antica raffigurazione di un Urobóros è stata rinvenuta nella tomba del faraone Tutankhamon. Successivamente, all’interno del movimento dello Gnosticismo, movimento filosofico, religioso ed esoterico, il serpente veniva spesso associato al Cristo. L’Urobóros è perfino il simbolo, in alchimia, della palingenesi, ossia il processo alchemico in seguito al quale si giunge a purificare una sostanza prima; si tratta perciò di una sorta di “trasmutazione”. Secondo uno di questi procedimenti si poteva ottenere la celebre Pietra filosofale, l’elisir dell’immortalità.

CROCE DI SAN BONIFACIO (700 d.C.): Un primo simbolo di infinito apparve nella cosiddetta “croce di San Bonifacio”, comparsa per la prima volta nel 700 d.C. Si tratta di una croce latina le cui braccia sono appunto avvolte da un otto sdraiato.

L’“OTTO ROVESCIATO” DI JOHN WALLIS (1655 d.C.): John Wallis, matematico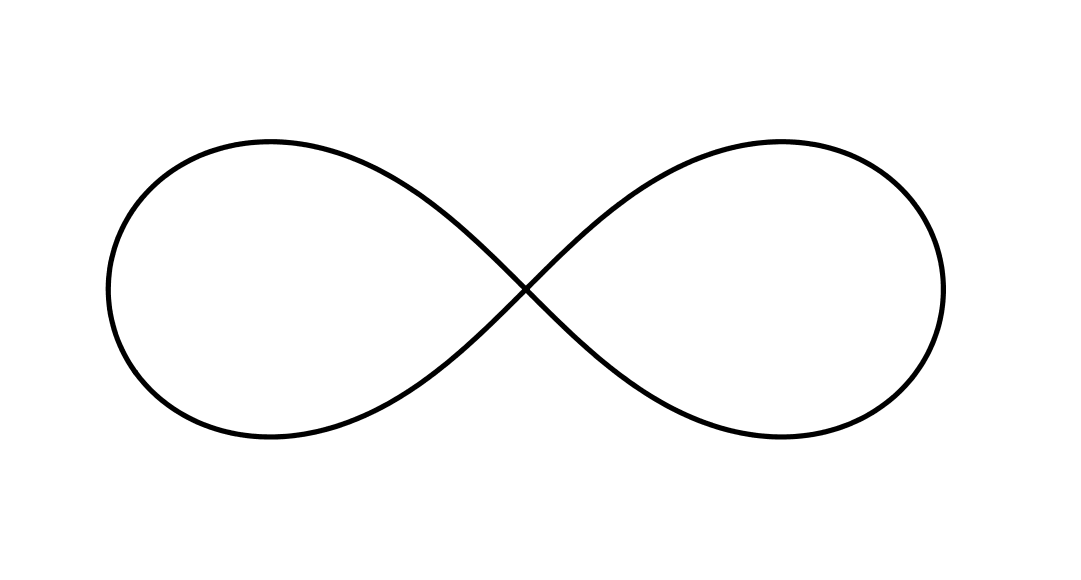  originario di Oxford a cui dobbiamo anche un contributo nell’ambito del calcolo del pi greco, fu il primo a servirsi del nastro disposto a forma di otto rovesciato per scopi matematici. Pare che egli riprese dal sistema di notazione romano il numero    C I Ɔ (usato in qualche caso al posto di M, per indicare il valore di 1000), divenuto poi  CƆ e infine ∞, ottenuto anche semplicemente

tracciando il segno più rapidamente. Sicuramente, all’epoca dei Romani il numero mille doveva rappresentare una quantità molto elevata, tanto è vero che alle volte veniva adoperato per intendere molto genericamente “tanti”.                                           Una variante di questo simbolo, è quella, molto simile, ideata da Eulero. Egli decise di tracciare un simbolo leggermente differente per poter conferire a quest’ultimo l’accezione di “infinito assoluto”. Ciò che varia sono le linee, che non sono continue, ma lasciano il simbolo “aperto”, come si può vedere nell’immagine. Questo simbolo, in ogni caso, non è più in uso.

 

LA LEMNISCATA (1696 d. C.): Introdotta da Jacob Bernoulli, si tratta di una curva descritta da precise 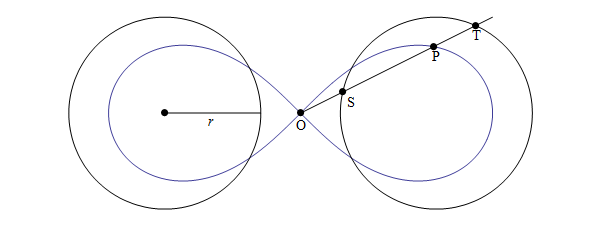coordinate cartesiane. Il matematico concepì tale curva come una modificazione dell’ellisse, figura geometrica che si ottiene da una costante somma delle distanze dai fuochi (due punti fissi). Una lemniscata prevede invece che il prodotto delle distanze sia costante. Bernoulli chiamò tale simbolo “lemniscus”, che nel mondo romano designava un nastro ornamentale per corone.

Follow Ápeiron on Instagram: