“Arrivo, ora, all’ineffabile centro del mio racconto; comincia, qui, la mia disperazione di scrittore. Ogni linguaggio è un alfabeto di simboli il cui uso presuppone un passato che gl’interlocutori condividono; come trasmettere agli altri l’infinito Aleph, che la mia timorosa memoria a stento abbraccia? […]

Nella parte inferiore della scala, sulla destra, vidi una piccola sfera cangiante, di quasi intollerabile fulgore. Dapprima credetti ruotasse; poi compresi che quel movimento era un’illusione prodotta dai vertiginosi spettacoli che essa racchiudeva. Il diametro dell’Aleph  sarà stato di due o tre centimetri, ma lo spazio cosmico vi era contenuto, senza che la vastità ne soffrisse. Ogni cosa (il cristallo dello specchio, ad esempio) era infinite cose, poiché io la vedevo distintamente da tutti i punti dell’universo. Vidi il popoloso mare, vidi l’alba e la sera, vidi le moltitudini d’America, vidi un’argentea ragnatela al centro d’una nera piramide, vidi un labirinto spezzato (era Londra), vidi infiniti occhi vicini che si fissavano in me come in uno specchio, vidi tutti gli specchi del pianeta e nessuno mi rifletté, vidi in un cortile interno di via Soler le stesse mattonelle che trent’anni prima avevo visto nell’andito di una casa di Fray Bentos, vidi grappoli, neve, tabacco,  vene di metallo, vapor d’acqua, vidi convessi deserti equatoriali e ciascuno dei loro granelli di sabbia, vidi ad Inverness una donna che non dimenticherò, vidi la violenta chioma, l’altero corpo, vidi un tumore nel petto, vidi un cerchio di terra secca in un sentiero, dove prima era un albero, vidi in una casa di Adrogué un primo esemplare della prima versione di Plinio, quella di Philomen Holland, vidi contemporaneamente ogni lettera di ogni pagina (bambino, solevo meravigliarmi del fatto che le lettere di un volume chiuso non si mescolassero e perdessero durante la notte), vidi insieme il giorno e la notte di quel giorno, vidi un tramonto a Querétaro che sembrava riflettere il colore di una rosa nel Bengala, vidi la ma stanza da letto vuota, vidi in un gabinetto di Alkmaar un globo terracqueo posto tra due specchi che lo moltiplicano senza fine, vidi cavalli dalla criniera al vento, su una spiaggia del mar Caspio all’alba, vidi la delicata ossatura d’una mano, vidi i sopravvissuti a una battaglia in atto di mandare cartoline, vidi in una vetrina di Mirzapur un mazzo di carte spagnolo, vidi le ombre oblique di alcune felci sul pavimento di una serra, vidi tigri, stantuffi, bisonti, mareggiate ed eserciti, vidi tutte le formiche che esistono sulla terra, vidi un astrolabio persiano, vidi un cassetto della scrivania (e la calligrafia mi fece tremare)  lettere impudiche, incredibili, precise che Beatriz aveva diretto a Carlos Argentino, vidi un’adorata tomba alla Chacarita, vidi il resto atroce di quanto deliziosamente era stata Beatriz Viterbo [l’amata del protagonista, cugina di Argentino], vidi la circolazione del mio oscuro sangue, vidi il meccanismo dell’amore e la modificazione della morte, vidi l’Aleph, da tutti i punti, vidi nell’Aleph la terra e nella terra di nuovo l’Aleph e nell’Aleph la terra, vidi il mio volto e le mie viscere, vidi il tuo volto, e provai vertigini e piansi, poiché i miei occhi avevano visto l’oggetto segreto e supposto, il cui nome usurpano gli uomini, ma che nessun uomo ha contemplato: l’inconcepibile universo”.

 Il problema della topografia: La topologia, a differenza della geometria, viene alterata soltanto nel caso in cui la superficie subisca uno strappo o viene forata, o anche se vengono incollate assieme due parti distinte dello spazio.

Prendiamo un foglio e disegniamovi un triangolo equilatero (la somma dei suoi angoli interni è di 180°). Ora, se lo avvolgiamo a formare un cilindro, incollando le due estremità, sapremo che si tratta sempre dello stesso triangolo: esso ha quindi una somma degli angoli interni sempre pari a 180°, e non maggiore (se la curvatura è verso l’infuori la somma degli angoli interni dovrebbe invece essere maggiore di 180°). Dunque anche il cilindro ha una geometria piana! L’unica differenza tra i due è di tipo topologico.

Se si applica l’esempio illustrato nella didascalia della precedente immagine all’universo, si può dunque concludere che è possibilissimo che l’universo possa continuare ad estendersi illimitatamente, pur non essendo infinito, e continuando a preservare una superficie piana (quella del cono). Si pensa dunque che parlare di topologie finite sia molto più calzante rispetto a quelle infinite. Per quanto non si sappia con certezza se l’universo corrisponda alla descrizione di una topologia finita, le recenti osservazioni compiute dal satellite WMAP potrebbero fornirne una prova. 

Il problema dell’uniformità: Dobbiamo fare i conti con una grande limitazione: per noi è possibile osservare soltanto una frazione, chissà quanto piccola!, dell’universo; figurarsi poi se l’universo fosse infinito: quanto conosciamo sarebbe praticamente nulla! La nostra conoscenza finita dell’universo è dovuta al fatto che la luce viaggi ad una velocità finita (e non infinita come sosteneva Newton). Secondo la “teoria dell’inflazione”, molto gettonata in ambito cosmologico, è probabile che l’universo osservabile sia molto diverso da quello invisibile a noi. L’ipotesi formulata da E. Borel è che le regioni dell’universo abbiano subito delle espansioni in maniera disomogenea: per qualcuna l’espansione era avvenuta più rapidamente di altre (il fenomeno potrebbe essere paragonato ad un gruppo di palloncini, alcuni gonfiati con più lentezza, altri con più celerità). È possibile predire la distribuzione delle variazioni della disuniforme espansione dell’universo visibile, un singolo palloncino. E per quanto riguarda gli altri, magari in numero infinito? La fisica potrebbe addirittura cambiare di palloncino in palloncino. In conclusione, dobbiamo essere consapevoli che, pur vivendo in una porzione di universo di estensione finita, in cui vigono determinate leggi fisiche, vi sono tre dimensioni e quattro forze, questa porzione potrebbe far parte di un tutto non solo infinito, ma di cui essa non è neppure una “riproduzione in piccolo”, poiché le cose, là fuori, potrebbero essere molto diverse. E se così fosse, non potremo mai sapere se l’universo è finito o infinito.

Il problema dell’accelerazione: gli astronomi hanno di recente scoperto che i corpi che si trovano ai margini dell’universo osservabile tendono ad espandersi (e quindi a distanziarsi l’un l’altro) con una velocità accelerata, e ciò va contro le previsioni: l’andamento che era stato pronosticato per l’espansione dell’universo era una costante decelerazione, dovuta alla forza di gravità. Come si spiega dunque quell’accelerazione? Dev’esservi un’energia oscura che compie una funzione “anti-gravitazionale”, repulsiva, abbondantemente presente nell’universo (circa il 70% dell’energia totale). Se, come sembra, quest’espansione avrà una durata infinita, l’universo apparrà desolato, e l’universo naturalmente sarà infinito da un punto di vista temporale, quanto alla sua infinitudine spaziale essa coinciderà ad una sorta di infinito potenziale (la distanza tra due oggetti può sempre aumentare, come nella successione di numeri naturali: 1, 2, 3, 4, …). Non è da escludere neppure la possibilità che, in qualche modo l’energia oscura si dissolva, ma in questo momento non si possiedono certezze in merito.

Vari sono i simboli nei quali è racchiuso il concetto d’infinito, che tende a sfuggire alla nostra comprensione. La forma di “otto sdraiato”, così come la conosciamo, e adoperata nel mondo matematico, fu ideata da John Wallis, ma già in precedenza esistevano simboli molto simili a quello noto a tutti, ossia “∞”.Vediamo di ripercorrere in rassegna la “storia della notazione” di tale concetto.

UROBÓROS (1600 a.C.): Una prima rappresentazione del concetto di infinito si può trovare nel cosiddetto “Urobóros”, simbolo antichissimo, diffusosi in diverse culture, dalla storia molto interessante. Il termine è di derivazione greca, e significa “serpente che si morde la coda”. Dunque, per quanto riguarda la rappresentazione, esso raffigura un drago, o un serpente che, nel mordersi la coda, forma un circolo, che non ha né inizio né fine. In effetti, il simbolo si rivela particolarmente efficace: esso rappresenterebbe l’infinito come un ripetersi incessante di tutte le cose. Il serpente che si divora infatti indica la disgregazione e al contempo la rinascita. La natura ciclica delle cose era particolarmente cara ai popoli precristiani, in particolare a quelli orientali. Basti pensare alla teoria del divenire del filosofo Eraclito (del pánta rheî), o quella di Anassimandro. Per questo motivo, il simbolo rappresenta l’unità primigenia, la totalità del tutto, e dunque anche l’infinito. Tale simbolo potrebbe ben rappresentare anche la teoria dell’ “eterno ritorno” del filosofo Nietzsche.                                                                                                                       La più antica raffigurazione di un Urobóros è stata rinvenuta nella tomba del faraone Tutankamon. Successivamente, all’interno del movimento dello Gnosticismo, movimento filosofico, religioso ed esoterico, il serpente veniva spesso associato al Cristo. L’Urobóros è perfino il simbolo, in alchimia, della palingenesi, ossia il processo alchemico in seguito al quale si giunge a purificare una sostanza prima; si tratta perciò di una sorta di “trasmutazione”. Secondo uno di questi procedimenti si poteva ottenere la celebre Pietra filosofale, l’elisir dell’immortalità.

Su un compendio alchemico del 1706 si trova un
Urobóros doppio. Poiché durante il processo alchemico della trasmutazione la Materia Prima si divide nei suoi principi costitutivi, l’Urobóros alchemico viene spesso rappresentato anche nella forma di due serpenti che si rincorrono le code. Interessante notare che tale rappresentazione richiami molto quella d’infinito a forma di “otto rovesciato”.

Talismano “Auryn”,
tratto da “La storia infinita” di M. Ende,
che si rifà al simbolo dell’Ourobóros.

CROCE DI SAN BONIFACIO (700 d.C.): Un primo simbolo di infinito apparve nella cosiddetta “croce di San Bonifacio”, comparsa per la prima volta nel 700 d.C. Si tratta di una croce latina le cui braccia sono appunto avvolte da un otto sdraiato.

L’“OTTO ROVESCIATO” DI JOHN WALLIS (1655 d.C.): Il matematico John Wallis, originario di Oxford, fu il primo a servirsi del nastro disposto a forma di otto rovesciato per scopi matematici. Pare che egli riprese dal sistema di notazione romano il numero    C I Ɔ (usato in qualche caso al posto di M, per indicare il valore di 1000), divenuto poi  CƆ e infine ∞, ottenuto anche semplicemente tracciando il segno più rapidamente. Sicuramente, all’epoca dei Romani il numero mille doveva rappresentare una quantità molto elevata, tanto è vero che alle volte si adoperava per intendere molto genericamente “tanti”.                                                           Una variante di questo simbolo, è quella, molto simile, ideata da Eulero. Egli decise di tracciare un simbolo leggermente differente per poter conferire a quest’ultimo l’accezione di “infinito assoluto”. Ciò che varia sono le linee, che non sono continue, ma lasciano il simbolo “aperto”, come si può vedere nell’immagine. Questo simbolo, in ogni caso, non è più in uso.

Simbolo dell’infinito così come lo tracciò L. Eulero.

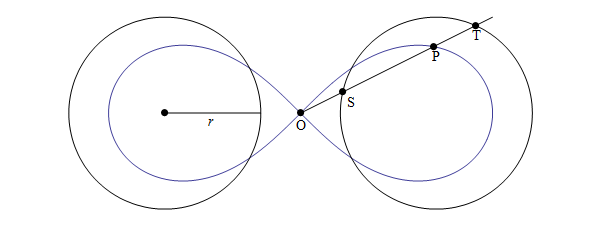LA LEMNISCATA (1696 d. C.): Introdotta da Jacob Bernoulli, curva descritta da precise coordinate cartesiane. Il matematico concepì tale curva come una modificazione dell’ellisse, figura geometrica che si ottiene da una costante somma delle distanze dai fuochi (due punti fissi). Una lemniscata prevede invece che il prodotto delle distanze sia costante. Bernoulli chiamò tale simbolo “lemniscus”, che nel mondo romano designava un nastro ornamentale per corone.