Quando uno scarafaggio cieco si trascina sulla superficie di un ramo piegato, in realtà non si rende conto che il tracciato che percorre è una curva. Ho avuto la fortuna di capire ciò che lo scarafaggio ignorava”.
Risposta di Einstein al figlio Eduard, che gli domandò perché fosse diventato così famoso.
Come abbiamo visto, Cantor e i suoi predecessori hanno in qualche modo aperto la strada dell’infinito, o meglio degli infiniti matematici, offrendocene una descrizione chiara; al giorno d’oggi, trattare gli infiniti attuali non costituisce più un’operazione problematica in matematica.
Volendo invece considerare l’infinito da un punto di vista fisico, la questione si fa più complessa. L’infinito matematico, in fin dei conti, non va a ricercare un’applicazione nella realtà, mentre l’infinito fisico può avere delle importanti conseguenze sull’universo; dall’altro canto quindi, è anche molto più spettacolare ed affascinante. Ecco cosa scriveva Cantor:
“L’infinito attuale si presenta in tre contesti: primo, quando viene realizzato nella forma più completa in un essere ultraterreno pienamente indipendente, in Deo, nel secondo caso lo chiamo infinito assoluto, o semplicemente assoluto; secondo, quando si manifesta nel mondo contingente, creato; terzo, quando la mente lo afferra in abstracto nella forma di una grandezza matematica, di un numero o di un tipo di ordine. Voglio distinguere nettamente tra l’assoluto e ciò che chiamo il transfinito, cioè gli infiniti attuali degli ultimi tipi, che sono chiaramente limitati, soggetti a ulteriore incremento, e quindi correlati con il finito”.
Dunque Cantor distingueva tre tipi di infinito: l’infinito assoluto (che coincideva con Dio), gli infiniti matematici (ossia i numeri transfiniti) e quelli fisici (costituiti dagli infiniti presenti nell’universo fisico). Per quanto riguarda quest’ultima categoria però, bisogna precisare che Cantor era dell’opinione che l’universo fosse finito, per età ed estensione, opinione assolutamente inusuale ai suoi tempi.
Tutte le leggi fisiche esistenti fino al XX secolo prevedevano l’esistenza di uno spazio tridimensionale in cui il tempo scorreva “indisturbato“, cioè senza che mai esso fosse influenzato da qualsiasi tipo di fenomeno; così anche per lo spazio.
“Due cose sono infinite: l’universo e la stupidità umana, ma riguardo l’universo ho ancora dei dubbi”.
Albert Einstein
 Successivamente Einstein, con le sue geniali intuizioni, riuscì a trovare un nesso tra spazio e tempo, assieme alla forza di gravità. Così, la geometria dello spazio e il ritmo con cui fluisce il tempo secondo la concezione newtoniana furono drasticamente rivoluzionate. Lo spazio e il tempo non erano più fattori non condizionabili. Quando i corpi sono collocati nello spazio di Einstein, la loro massa e il loro moto plasmano la conformazione spaziale e il ritmo con cui il tempo scorre in luoghi diversi.
Successivamente Einstein, con le sue geniali intuizioni, riuscì a trovare un nesso tra spazio e tempo, assieme alla forza di gravità. Così, la geometria dello spazio e il ritmo con cui fluisce il tempo secondo la concezione newtoniana furono drasticamente rivoluzionate. Lo spazio e il tempo non erano più fattori non condizionabili. Quando i corpi sono collocati nello spazio di Einstein, la loro massa e il loro moto plasmano la conformazione spaziale e il ritmo con cui il tempo scorre in luoghi diversi.

Possiamo immaginare l’universo di Einstein come una coperta estremamente elastica.
Così, dove non vi è massa, lo spazio è quasi del tutto piatto, corrisponde ossia alla descrizione newtoniana. Al contrario, quando grandi quantità di massa si trovano in una non troppo estesa regione spaziale i corpi si muovono a velocità prossime a quella della luce, e lo spazio e il tempo si deformano. Per cui, se qualsiasi grandezza fisica dovesse raggiungere un valore infinito, potrebbero esservi delle significative ripercussioni, a partire dalla curvatura dello spazio, che diverrebbe appunto infinita: lo spazio verrebbe così lacerato. Questo tipo di situazione estrema è detta “singolarità“.

Rappresentazione di uno spazio curvo che evolve in una singolarità.
Dunque, potrebbe esistere una singolarità nell’universo? E, più in generale, è possibile osservare un infinito fisico? A questi interrogativi stanno tentando di rispondere studiosi come cosmologi, ingegneri e fisici delle particelle. Interessiamoci ora delle ricerche di questi ultimi.
I fisici delle particelle, che studiano i costituenti della materia e le interazioni fondamentali tra questi, si occupano appunto dell’infinitamente piccolo, analizzando particelle prodotte da acceleratori all’avanguardia. Ci troviamo all’opposto dell’infinitamente grande, ma, come ha affermato il fisico Guido Tonelli, “gli estremi si toccano”: infatti i fisici delle particelle studiano particelle in condizioni estreme, che sono molto vicine a quelle proprie dell’universo primordiale, ed ecco il punto di contatto tra l’infinitamente grande e l’infinitamente piccolo.
Ad ogni modo, per lungo tempo i fisici si sono imbattuti in quantità infinite in calcoli di semplici grandezze fisiche, cosicché ci si prodigò al fine di superare questa difficoltà. Alla fine, la questione non fu chiusa, ma piuttosto elusa; si elaborò un metodo per scomporre il risultato in una parte finita ed una infinita, cosicché la parte finita potesse essere confrontata con altre osservazioni, mentre quella infinita semplicemente essere “messa in un canto” (lo stratagemma potrebbe essere paragonato all’uso delle incognite nell’algebra: non conoscendo una certa quantità, essa viene denominata ad esempio x, così da poter eseguire agevolmente calcoli come 4x-1x=3x). Questo procedimento è detto “rinormalizzazione” (esso, fra le altre cose, costituisce una conferma del bosone di Higgs). La “comparsa” degli infiniti indusse però a pensare che il sistema attraverso il quale si vedeva la realtà fosse inadeguato, come può esserlo guardare un cielo stellato attraverso una lente di ingrandimento, anziché adoperare un telescopio. Ad esempio, la cosiddetta “teoria delle stringhe“, ancora in fase di sviluppo, potrebbe consentirci di evitare questi scomodi infiniti mutando la concezione della natura dei mattoni elementari che costituiscono l’universo (l’importanza di simili teorie era stata, in un certo senso, già apprezzata dalla geniale mente di Immanuel Kant: si veda l’articolo “L’infinito è conoscibile?”). Anziché considerarli come “punti”, essi possono essere visti come degli anelli di energia, i quali, muovendosi, descrivono tubi nello spazio (e non linee come sarebbe per i punti). Queste corde, o stringhe, sono tese, proprio come un elastico, e si allentano via via che la temperatura sale; al contrario, se la temperatura diminuisce, gli anelli delle spire sono sempre più tesi, e quindi simili a punti: si tratta di un “ampliamento” della teoria puntiforme, poiché questo modello può andar bene in condizioni di basse temperature, ma non è appropriato in casi di alte temperature.
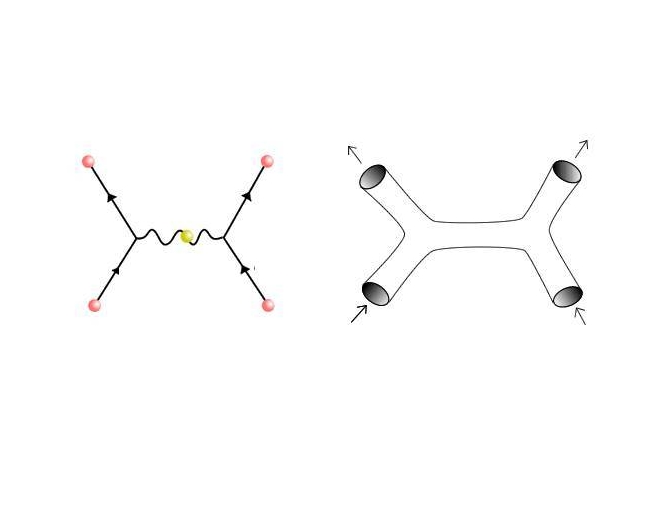
Nel primo caso, vediamo come due punti in movimento vadano a costituire delle linee; la loro interazione genera un punto che seguirà il loro moto nello spazio e nel tempo, ed è questo indice del fatto che un infinito si “paleserà” prima o poi nel calcolo di questa interazione. Nel secondo caso invece, l’intersecarsi dei due “tubi”, non potrà generare altro che una transizione continua a due altri tubi, e questa è garanzia del fatto che non si potrà incorrere in alcun infinito.
In ogni caso, i fisici sono piuttosto fiduciosi: si spera che questa teoria possa costituire una “teoria del tutto“. Essi propendono invece molto meno per credere che gli infiniti fisici esistano.
Follow Ápeiron on Instagram:



