Dopo essere giunti nella prima parte ad una vera e propria crisi del pensiero matematico, apriamo questa seconda parte con una personalità che, da un lato portò alla luce alcune questioni interessanti ma anche assai sconvolgenti, dall’altro, contribuì in qualche modo a rendere l’infinito matematico qualcosa di “sospetto”, di cui “diffidare”… stiamo parlando di Zenone di Elea.
I PARADOSSI DI ZENONE
Zenone di Elea fu discepolo ed amico del filosofo Parmenide, padre dell’ontologia. Quest’ultimo, aveva affermato che la realtà è una, e coincide con l'”essere” che è a sua volta, fra le altre cose, infinito, nell’accezione di “aspaziale”, ma anche finito, nell’accezione di “conchiuso”. I suoi oppositori avevano però asserito che se la realtà fosse una, ci si incaglierebbe inevitabilmente in ridicole contraddizioni. Così Zenone, per tutta risposta, sostenne che se la realtà fosse molteplice si incorrerebbe in contraddizioni ben più problematiche. Pertanto decise di prendere le difese del maestro sostenendo e dimostrando vari argomenti contro la pluralità.
I primi due argomenti, i più famosi, sono diretti alla confutazione del movimento inteso come realtà.
Primo argomento, detto “dello stadio”: secondo Zenone è impossibile arrivare all’estremità di uno stadio partendo dall’estremità opposta, poiché sarebbe necessario prima arrivare alla metà di esso, e ancor prima alla metà di questa metà, e così via, all’infinito. Ma non è possibile percorrere in un tempo finito infinite parti di spazio.
Secondo argomento, detto “dell’Achille”: in accordo con tale argomento, il “piè veloce” Achille non potrà mai raggiungere una tartaruga, qualora le avrà concesso un passo di vantaggio. Infatti, prima di raggiungerla, l’eroe dovrà arrivare alla posizione occupata in precedenza dalla tartaruga, la quale però si sarà nel frattempo spostata, seppur di pochissimo; ne consegue che la distanza tra i due non si ridurrà mai a zero, pur diventando sempre più piccola, tendendo così ad infinito.
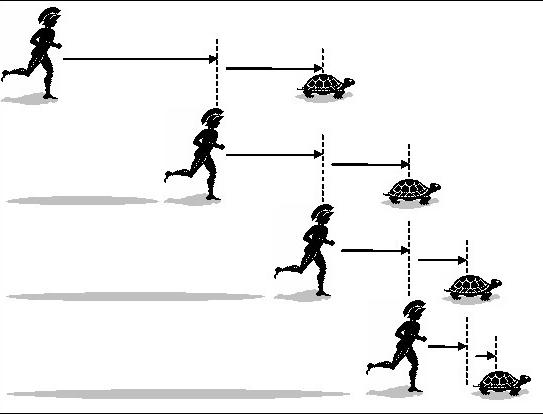
Supponiamo che la distanza tra Achille (A) e la tartaruga (T) sia pari a 1, e che tra le velocità di A e di T esista un rapporto di 100:1. Quando A avrà percorso il tratto 1, T sarà avanzato di 1/100, e quando A avrà percorso il tratto (1+1/100), T sarà avanzato di 1/100+(1/100 di 1/100); e così via. L’incontro tra A e T non potrà mai avvenire: A dovrebbe completare l’incompletabile.
RETTIFICAZIONE DEL CERCHIO
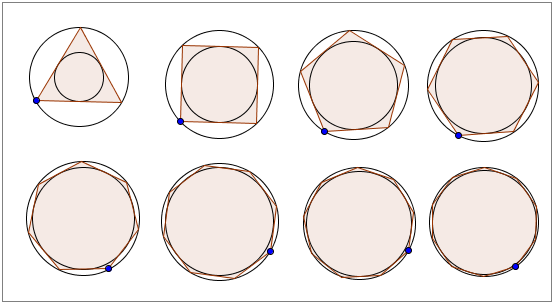
Si tratta di un problema geometrico, che consiste nel voler calcolare l’area del cerchio. Esso venne per la prima volta risolto da Eudosso di Cnido con un metodo rigoroso e del tutto corretto, il cosiddetto “metodo di esaustione“, che consente di calcolare l’area di determinate figure geometriche approssimandole con una serie di poligoni dai lati sempre più numerosi, ossia poligoni via via più simili al cerchio. Si può dunque asserire che il numero di lati dei poligoni tenda ad infinito, e che l’area cercata sia il limite di queste stesse aree (n lati→∞).
In vero, l’idea di circoscrivere ed inscrivere nella circonferenza dei poligoni per poi accrescerne il numero non era affatto nuova, solo non si era certi se, prima o poi, si sarebbe pervenuti ad una “figura ultima”. Come vedremo, Aristotele dissentì, sfruttando il concetto di “infinito potenziale”.
ARISTOTELE
Aristotele, uno dei più grandi filosofi di tutti i tempi, respinse l’idea di infinito. Egli era persuaso che l’universo fosse finito, ma a circondarlo era il vuoto infinito; ciò per poter giustificare il posto centrale che la Terra occupava nell’universo (teoria geocentrica), giacché se l’universo fosse stato infinito non sarebbe stato possibile determinarne un centro, che fosse peraltro unico.
Fu proprio Aristotele a tentare di correre ai ripari, a seguito della crisi degli irrazionali e dei paradossi di Zenone: egli effettuò una distinzione tra infiniti “potenziali” ed infiniti “attuali”. Un esempio di infinito in potenza è quello di una successione di numeri naturali: 1, 2, 3, 4, 5, 6, 7, 8, …: la successione è infinita, e sarà sempre possibile aggiungere uno. Ebbene, questo processo non sarà mai concluso, non si esprimerà mai nella sua totalità. Aristotele scartò del tutto la possibilità di un infinito in atto, mentre non escluse quella di un infinito potenziale, proprio come “processo di ecceterazione” (vale a dire la possibilità di andare sempre oltre). Dunque, secondo Aristotele, non avrebbe mai potuto verificarsi un infinito attuale. Così Aristotele giunse a ribaltare la concezione di Anassimandro, che intendeva l’infinito come un tutto, come perfezione e completezza: l’infinito è “non ciò al di fuori del quale non vi è nulla, ma ciò al di fuori del quale vi è sempre qualcosa”.
Naturalmente, quello di Aristotele, fu il primo audace tentativo di fronteggiare problemi alquanto complessi e insidiosi. Benché ad un lettore contemporaneo le sue conclusioni potranno parere assolutamente estranee ed inadeguate alla concezione moderna e scientifica di infinito, superate e quasi ingenue, va precisato che ai tempi del filosofo l’osservazione del mondo e dell’universo risultava notevolmente limitata, né si disponeva di strumenti adeguati. Egli, ad ogni modo, riuscì nell’intento di creare una ferrea coerenza in tutto il suo sistema filosofico, che rispondesse a quanto fosse osservabile.
“Il divino Aristotele e i suoi discepoli hanno mostrato a sufficienza che non esiste grandezza infinita in alcuna cosa nelle dimensioni sensibili. […] Ma non è ugualmente possibile che l’infinito sia nei concetti astratti e non divisibili”.
Proclo Licio Diadoco
Ma era veramente finita così? Vediamo nella terza parte quali furono gli sviluppi del concetto di infinito matematico in epoca moderna.
Follow Ápeiron on Instagram: