Nonostante fosse stato in parte superata la forma di “pregiudizio” che gravava sull’infinito matematico, esso tardava in ogni modo ad essere accettato dai matematici; spesso e volentieri, argomentazioni intorno agli infiniti conducevano a risultati sconcertanti e contrari a qualsiasi logica (perfino che 0=1!). Ancora forte era la tendenza a relegarli in un canto facendo finta che non esistessero, o a dichiararli direttamente inesistenti. Fu un uomo, nell’Ottocento, a dissipare una simile confusione ed incertezza, Georg Cantor. La sua teoria, con estrema chiarezza, andava a giustificare tutte quelle spiacevoli ambiguità in cui ci si era imbattuti fino a quel momento e, così, a spalancare le porte dell’infinito matematico una volta per tutte. Naturalmente, incontrò l’ostinatissima opposizione di molti, e ciò lo fece scivolare in un.

Infiniti numerabili: Cantor definì numerabile un infinito che potesse essere posto in corrispondenza biunivoca (per esemplificare questo concetto, potremmo paragonarlo agli armadietti numerati che vengono assegnati agli studenti: ad ogni studente corrisponde un armadietto ben preciso) con la successione dei numeri naturali. Per esempio i numeri pari sono numerabilmente infiniti (come illustrato dalla figura), così come i dispari.

Tutti gli infiniti numerabili possiedono la stessa cardinalità, ossia la stessa “grandezza”, “dimensione”, “numerosità”. Questi infiniti, per Cantor, sono attuali, più precisamente sono gli infiniti minimi che possono esistere. Per indicarli, adoperò la prima lettera dell’alfabeto ebraico, aleph con zero, , il primo numero cardinale transfinito (così venne definito dallo stesso Cantor). Da ciò deriva la cosiddetta “diagonale di Cantor”, con la quale il matematico dimostrò che anche l’insieme di tutte le frazioni ottenute dividendo un numero intero per un altro, come 7/8, ad esempio, è un infinito numerabile. Le conclusioni sono sorprendenti: contrariamente a quanto si potrebbe pensare, cioè che l’insieme delle frazioni sia più numeroso di quello dei numeri interi, il numero delle frazioni è uguale a quello dei numeri singoli! Dunque tutti gli infiniti considerati nell’antichità erano infiniti numerabili. Ma ce ne sono di altri.

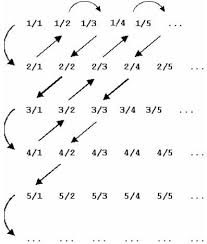
Secondo questo schema, numeratore e denominatore di ogni riga hanno la stessa somma (per 1/1 la somma è per numeratore e denominatore 2; per 2/1 e 1/2 la somma è sempre 3; per 3/1, 2/2 e 1/3 la somma è sempre 4; etc.).

Infiniti non numerabili: Cantor riuscì poi a dimostrare come siano possibili infiniti più grandi dei numerabili, appunto i “non numerabili”. I decimali (che comprendono gli irrazionali, o comunque numeri dalle cifre illimitate, i numeri periodici, e pertanto non possono essere scritti sotto forma di frazioni) non possono essere circoscritti alla stregua dei numeri pari e dispari, ad esempio: sono un infinito non numerabile. Il genio di Cantor riuscì a dimostrare ciò con una dimostrazione per assurdo. In conclusione, i decimali sono un insieme infinitamente maggiore di quello dei numerabili, ossia dei naturali, delle frazioni. Quindi, il “continuo”, di cui sopra, venne indicato con il simbolo , ed è anch’esso definito numero transfinito. Cantor credeva inoltre che non esistesse un infinito maggiore di  e minore di , senza però riuscire mai a dimostrarlo.

La scoperta di Cantor di infiniti di differente ordine di grandezza, ben distinguibili, fu qualcosa di rivoluzionario nella storia della matematica. Egli, in seguito scoprì che gli infiniti non solo sono numerabili, ma anche insuperabili. Non poteva esistere un “infinito più grande di tutti”, l'”infinito più infinito” che potesse ritenere tutti gli altri. Per provare ciò, Cantor aveva bisogno di dimostrare l’esistenza matematica (in matematica il concetto di “esistenza” non implica l’esistenza concreta, fisica, ma semplicemente una rigorosa coerenza logica) di questa successione interminabile di infiniti: era necessario prendere in considerazione l'”insieme potenza”, ovvero l’insieme che contiene tutti i sottoinsiemi di un determinato insieme infinito, nel nostro caso: se l’insieme di partenza ha n membri, i membri dell’insieme potenza avranno 2ⁿ elementi.

Da uomo di grande fede, Cantor era persuaso che l'”infinito assoluto” appartenesse esclusivamente a Dio. Era Dio a capeggiare la “gerarchia” degli infiniti infiniti; tuttavia questo infinito risultava inafferrabile per la mente umana.

Queste straordinarie idee, sicuramente frutto di una sconfinata immaginazione, oltre che di un altrettanto notevole genio, non tardarono ad essere accettate anche dai matematici, sfortunatamente soltanto in seguito alla triste morte del loro concepitore.

“L’infinito potenziale ha solo una realtà presa a prestito, dato che un concetto di infinito potenziale rimanda sempre a un concetto che lo procede logicamente e ne garantisce l’esistenza”.

Georg Cantor

“Achille”, Francesco Vallone, 2002

“La tartaruga”. Francesco Vallone, 2002

I PARADOSSI DI ZENONE:

Zenone di Elea fu discepolo ed amico del filosofo Parmenide, padre dell’ontologia. Quest’ultimo, aveva affermato che la realtà è una, e coincide con l'”essere” che è a sua volta, fra le altre cose, infinito, nell’accezione di “aspaziale”, ma anche finito, nell’accezione di “conchiuso”. I suoi oppositori avevano però asserito che se la realtà fosse una, ci si incaglierebbe inevitabilmente in ridicole contraddizioni. Così Zenone, per tutta risposta, sostenne che se la realtà fosse molteplice si incorrerebbe in contraddizioni ben più problematiche. Pertanto decise di prendere le difese del maestro sostenendo e dimostrando vari argomenti contro la pluralità.

I primi due argomenti, i più famosi, sono diretti alla confutazione del movimento inteso come realtà.

Primo argomento, detto “dello stadio”: secondo Zenone è impossibile arrivare all’estremità di uno stadio partendo dall’estremità opposta, poiché sarebbe necessario prima arrivare alla metà di esso, e ancor prima alla metà di questa metà, e così via, all’infinito. Ma non è possibile percorrere in un tempo finito infinite parti di spazio.

Secondo argomento, detto “dell’Achille”: in accordo con tale argomento, il “piè veloce” Achille non potrà mai raggiungere una tartaruga, qualora le avrà concesso un passo di vantaggio. Infatti, prima di raggiungerla, l’eroe dovrà arrivare alla posizione occupata in precedenza dalla tartaruga, la quale però si sarà nel frattempo spostata, seppur di pochissimo; ne consegue che la distanza tra i due non si ridurrà mai a zero, pur diventando sempre più piccola, tendendo così ad infinito.

Supponiamo che la distanza tra Achille (A) e la tartaruga (T) sia pari a 1, e che tra le velocità di A e di T esista un rapporto di 100:1. Quando A avrà percorso il tratto 1, T sarà avanzato di 1/100, e quando A avrà percorso il tratto (1+1/100), T sarà avanzato di 1/100+(1/100 di 1/100); e così via. L’incontro tra A e T non potrà mai avvenire: A dovrebbe completare l’incompletabile.

RETTIFICAZIONE DEL CERCHIO:

Si tratta di un problema geometrico, che consiste nel voler calcolare l’area del cerchio. Esso venne per la prima volta risolto da Eudosso di Cnido con un metodo rigoroso e del tutto corretto, il cosiddetto “metodo di esaustione“, che consente di calcolare l’area di determinate figure geometriche approssimandole con una serie di poligoni dai lati sempre più numerosi, ossia poligoni via via più simili al cerchio. Si può dunque asserire che il numero di lati dei poligoni tendano ad infinito, e che l’area cercata sia il limite di queste stesse aree (n lati→∞).

In vero, l’idea di circoscrivere ed inscrivere nella circonferenza dei poligoni per poi accrescerne il numero non era affatto nuova, solo non si era certi se, prima o poi, si sarebbe pervenuti ad una “figura ultima”. Come vedremo, Aristotele dissentì, sfruttando il concetto di “infinito potenziale”.

ARISTOTELE:

Aristotele, uno dei più grandi filosofi di tutti i tempi, respinse l’idea di infinito. Egli era persuaso che l’universo fosse finito, ma a circondarlo era il vuoto infinito; ciò per poter giustificare il posto centrale che la Terra occupava nell’universo (teoria teocentrica), giacché se l’universo fosse stato infinito non sarebbe stato possibile determinarne un centro, che fosse peraltro unico.

Fu proprio Aristotele a tentare di correre ai ripari, a seguito della crisi degli irrazionali e dei paradossi di Zenone: egli effettuò una distinzione tra infiniti “potenziali” ed infiniti “attuali”. Un esempio di infinito in potenza è quello di una successione di numeri naturali: 1, 2, 3, 4, 5, 6, 7, 8, …: la successione è infinita, e sarà sempre possibile aggiungere uno. Ebbene, questo processo non sarà mai concluso, non si esprimerà mai nella sua totalità. Aristotele scartò del tutto la possibilità di un infinito in atto, mentre non escluse quella di un infinito potenziale, proprio come “processo di ecceterazione” (vale a dire la possibilità di andare sempre oltre). Naturalmente, secondo Aristotele, un infinito potenziale non avrebbe mai potuto verificarsi un infinito attuale. Così Aristotele giunse a ribaltare la concezione anassagorea, che intendeva l’infinito come un tutto, come perfezione e completezza: l’infinito è “non ciò al di fuori del quale non vi è nulla, ma ciò al di fuori del quale vi è sempre qualcosa”.

Naturalmente, quello di Aristotele, fu il primo audace tentativo di fronteggiare problemi alquanto intricato. Benché ad un lettore contemporaneo le sue conclusioni potranno parere assolutamente estranee ed inadeguate alla concezione moderna e scientifica di infinito, superate e quasi ingenue, va precisato che ai tempi del filosofo l’osservazione del mondo e dell’universo risultava notevolmente limitata, né si disponeva di strumenti adeguati. Egli, ad ogni modo, riuscì nell’intento di creare una ferrea coerenza in tutto il suo sistema filosofico, che rispondesse a quanto fosse osservabile.

“Il divino Aristotele e i suoi discepoli hanno mostrato a sufficienza che non esiste grandezza infinita in alcuna cosa nelle dimensioni sensibili. […] Ma non è ugualmente possibile che l’infinito sia nei concetti astratti e non divisibili”.

Proclo Licio Diadoco

Ma era veramente finita così?

“Noi sappiamo che c’è un infinito e ne ignoriamo la natura. Poiché sappiamo che è falso che i numeri sono finiti, è vero dunque che c’è un infinito nel numero. Ma non sappiamo che cosa è”.

Blaise Pascal

Come si è visto nel precedente articolo, la civiltà greca non riuscì ad accettare il concetto di infinito, in particolare in ambito matematico, tentando in ogni modo di esorcizzarlo. Non mancarono certo i tentativi di riconciliazione, tuttavia essi furono pregiudicati dalla consapevolezza dei fastidiosi problemi che i paradossi di Zenone erano in grado di originare.

In generale, con l’avvento del Cristianesimo, e con la diffusione del monoteismo, l’idea dell’infinito non fu più invisa. Sant’Agostino, ad esempio  sosteneva che quanto è infinito per l’uomo appare agli occhi di Dio finito. Nel Rinascimento, gli attributi assegnati a Dio erano in primis l’essere e l’infinità. Non senza qualche sottile criticità, si tendeva a far coincidere Dio stesso con l’infinito. O meglio, per non rischiare di giungere alla conclusione che Dio sia finito, qualora si fosse riusciti a circoscrivere l’infinito, i teologi non facevano coincidere Dio con l’infinito in senso essenziale e stretto. Naturalmente, ciò non voleva dire che Dio fosse finito, ma semplicemente consentiva di esulare le sorti dell’infinito, qualora fosse stato “imbrigliato” nelle reti dei matematici, dalla concezione di Dio, che così sarebbe rimasta intatta.

GALILEO: 

Galileo Galilei fu tra i primi a riuscire a valicare la barriera che pregiudicava un qualsiasi contatto tra l’uomo e l’infinito. In breve questo il suo pensiero: un qualunque oggetto limitato può essere ricondotto ad infiniti elementi privi di estensione e quindi indivisibili: se così non fosse, se queste parti fossero dotate di estensione, sarebbero anche divisibili, e dunque come si spiegherebbe la limitatezza del segmento?

La conclusione a cui perviene Galileo attraverso il cosiddetto “paradosso dei quadrati” è che non è possibile considerare l’infinito come i comuni numeri. Tuttavia è possibile effettuare un’operazione: si può, dati due insiemi infiniti, confrontarli e determinare se essi hanno lo stesso numero di elementi, creando una biezione tra l’uno e l’altro (dati due insiemi, A e B, si parla di corrispondenza biunivoca se  ad ogni elemento di A corrisponde uno ed uno solo elemento di B, e viceversa).

NEWTON E LIEBNIZ:

Con l’avvento del calcolo differenziale di Newton e Liebniz, l’infinito potenziale tornò in auge. Per distinguere gli infiniti dagli infinitesimi, adoperarono due diverse notazioni, rispettivamente il simbolo ∞ e il simbolo dt.

DEDEKIND:

Grazie a Richard Dedekind, che studiò l’infinito potenziale, due fondamentali problemi, ossia la questione degli irrazionali e quella del “continuo“.

Secondo Liebniz e Newton, la continuità dei punti di una retta si doveva far derivare dalla loro densità (proprietà secondo la quale un ulteriore punto potrà sempre trovarsi tra altri due punti), e tale caratteristica apparteneva anche ai numeri razionali. Tuttavia, questi ultimi non costituivano un “continuo” (come suggerisce il nome, un “continuo” è un insieme in cui gli elementi si susseguano in maniera densa, ma senza alcuna interruzione, senza “buchi”), poiché tra essi potevano essere frapposti numeri non razionali; lo si può notare anche dalla sottostante figura:

Proiezione sulla retta dei numeri della diagonale di un quadrato, che appunto corrisponde a √2, un numero irrazionale, e che dunque crea un’interruzione nella successione dei numeri razionali.

Così, Dedekind escogitò un ingegnosissimo “stratagemma”, che avrebbe risolto in un’unica soluzione i due grandi problemi. Egli considerò numeri come ad esempio √2, anziché delle “interruzioni”, degli “intoppi”, come una sorta di “spartiacque” tra una “successione continua” di numeri razionali ed un’altra. Quindi, un numero irrazionale, che fa pur sempre parte dell’insieme dei numeri reali, definisce una “sezione”, detta appunto di Dedekind in due insiemi, A e B, dove A è dato da tutti i razionali a tali che a<√2, e B è invece costituito da tutti i razionali b tali che b>√2 (per riassumere ulteriormente a<√2<b). In questo modo l’insieme dei numeri reali è visto come un’estensione dell’insieme dei razionali.

Rappresentazione degli insieme dei numeri reali con i suoi sottoinsiemi

Grazie a questa inedita definizione non vi sarebbe più stato bisogno di ricorrere al concetto di densità per poter definire a quello di continuità.

“La matematica è la scienza dell’infinito”. 

Hermann Weyl

Sin dall’antichità, il concetto di infinito è riuscito ad affascinare, ma anche turbare, in qualche modo, sicure e ben costruite concezioni, basate sul fatto che la ragione umana fosse in grado di comprendere, di concepire ogni forma di conoscenza, ogni entità. Per tale ragione l’infinito matematico non fu spesse volte accettato, o comunque catalogato in maniera pragmatica e messo in un canto in modo sbrigativo. Asserire che l’infinito fosse attuale, e non, al limite, potenziale, per alcuni avrebbe potuto suonare come assurdo, se non quasi empio, semplicemente, impossibile. Nel corso poi dei secoli, grazie alle ricerche di numerosi studiosi, anche l’infinito ha trovato un posto nella matematica.

Ogni epoca ha adottato un differente “atteggiamento” nei confronti dell’infinito matematico. Vediamo di ripercorrere, in breve, le tappe più salienti della storia dell’infinito matematico.

GLI ALBORI DELLA CIVILTÀ ELLENICA:

Ben noto è lo spirito ellenico per essere caratterizzato da una tale curiosità, da spingere sempre a compiere quel passo in più sulla strada della conoscenza, da sfidare le leggi della natura. Già i poemi omerici, in particolare l’Odissea, ci narrano di un popolo costantemente attratto dall’ignoto. Pensiamo ad Odisseo, detto “polýtropon“, ossia, secondo una delle tante accezioni, “rivolto in molte direzioni”, “versatile”, a tal punto da dimostrare una condotta spregiudicata, pur di pervenire alla conoscenza. Altri elementi contenuti nei poemi omerici suggeriscono l’infinitamente grande, come ad esempio la moltitudine degli astri, o le profondità del Tartaro. Come si spiega allora il fatto che l’infinito fosse per lo più inviso a questa civiltà?

Ciò non si può motivare se non con il fatto che in un primo periodo il rapporto con l’infinito non era così critico come divenne in seguito.

“Non c’è un minimo tra le cose piccole né un massimo tra le grandi, ma sempre qualcosa di ancora più piccolo e qualcosa di ancora più grande”.    

Anassimandro

Il filosofo Anassimandro individuò il principio di tutte le cose proprio in quello che chiamò ápeiron, ossia una sorta di materia primordiale in cui in principio ogni cosa conviveva, priva di forma ed indistinta: nella sua concezione ápeiron è sinonimo di “indeterminato“, interpretabile sia in senso spaziale, sia in senso quantitativo. In seguito si verificava la “separazione dei contrari“, ossia quel processo, dovuto ad una colpa non ben determinata, insita in tutte le cose, che avrebbe visto la separazione di tutti gli elementi opposti, come la luce e le tenebre, il giorno e la notte, che tendevano a sopraffarsi a vicenda, provocando ingiustizie. Tale stato di cose imperfetto verrà espiato con la distruzione di ogni cosa, che ritornerà all’ápeiron; per cui, secondo Anassimandro la perfezione coincideva con questa materia indeterminata ed infinita, mentre l’imperfezione con tutte le cose finite. Ad ogni modo, il processo di separazione dei contrari e di “ritorno all’infinito” è un processo ciclico, dunque infinito. Inoltre, visto questo eterno movimento e mutamento, non si può escludere che Anassimandro sostenesse l’infinità dei mondi, oltre che nel succedersi nel tempo, anche allo stesso tempo, quindi un infinito non solo nel tempo, ma perfino nello spazio.

Tuttavia, maggiormente accresceva l’inclinazione razionale dei Greci, meno diveniva accettabile il concetto di infinito…

I PITAGORICI:

La civiltà, il gusto greco si indirizzava sempre più verso l’armonia, l’equilibrio delle proporzioni, alla ricerca della perfezione. In generale, la perfezione, secondo i Greci, era raggiungibile, o quantomeno avvicinabile unicamente attraverso l’uso della ragione (o lógos). Ora, tutto ciò che non potesse essere compreso dalla ragione, veniva semplicemente considerato imperfetto.

Partendo da questa presupposto, possiamo comprendere come accettare una simile identità risultava sempre più improponibile alla mentalità di questo popolo. La stessa parola con la quale essi indicavano l’infinito, ossia ápeiron è una parola non descrittiva, priva di “sapore”. Infatti, il termine è composto “péirar”, “fine”, “limite”, preceduto dal prefisso “a-“, che sta per “privo di”. Dunque, è come se con tale termine i Greci intendessero non definire questa entità per quello che è, ma per quello che non è. L’infinito era ad essi inviso almeno quanto lo zero, che rendeva “il nulla” qualcosa: una cosa inesistente diveniva esistente. L’infinito sembrava inevitabilmente essere connesso proprio al concetto di “nulla”.

Pitagorici celebrano il sorgere del sole, Fëdor Bronnikov, 1869

In particolare, i Pitagorici, ai quali si deve una delle più grandi conquiste dell’umanità, la fondazione della matematica come scienza, lasciarono un’impronta decisiva per quanto riguarda la futura concezione d’infinito. Essi effettuarono una divisione dualistica del numero, considerato come un entità materica, in pari e dispari (è da questa opposizione che derivano tutte le altre presenti nel mondo). Il dispari è, nella sua stessa essenza, un’entità limitata, terminata, compiuta. Il pari invece è un’entità illimitata.

Come si può notare dalle figure, a differenza di quanto accade per i numeri dispari, non vi è alcun “punto” ad ostacolare le frecce, né vi è alcun termine che circoscriva e limiti lo spazio interno.

Per cui i numeri pari erano la rappresentazione fondamentale di tutto ciò che è difettoso. Lo stesso universo era da essi visto come il trionfo del finito sull’infinito, e parallelamente dell’ordine (non a caso l’universo veniva definito kósmos, che voleva anche dire “ordine”) sul disordine.

LA CRISI:

Secondo la concezione pitagorica, l’intera vita del cosmo  è retta da leggi esprimibili mediante rapporti numerici, ma proprio questa convinzione comportò la stessa crisi del pensiero pitagorico.

Come è noto, a Pitagora si attribuisce il celebre teorema per cui, in un triangolo rettangolo rettangolo, il quadrato costruito sull’ipotenusa è uguale alla somma dei quadrati costruiti sui cateti.

Ecco una dimostrazione originale ed immediata del Teorema di Pitagora, realizzata da A. De Lella

Sulla base di tale teorema i Pitagorici si trovarono di fronte alla sfida di determinare il rapporto tra la diagonale e il lato di un quadrato. Inevitabilmente, essi scoprirono che esso non corrispondeva né a una frazione tra numeri interi, né tantomeno ad un numero intero, ma a √2! Pur avendo lì, sotto gli occhi il segmento in questione, il suo valore, corrispondente a √2, non poteva essere calcolato se non con approssimazioni via via maggiori, tendenti all’infinito.

Un approssimazione della √2

La scoperta di grandezze tra loro incommensurabili, ovvero il lato e la diagonale di un quadrato, quasi come fossero incomunicabili fra loro, decretò un vero e proprio scandalo, a cui seguì la fine della concezione pitagorica del numero, ma aprì anche le porte alla speculazione in ambito filosofico e matematico a proposito dell’infinito, e così, la divisibilità all’infinito, rappresentata da tutte le cifre che in √2 vengono dopo la radice, divenne uno dei più grandi problemi per il pensiero greco.